The mathematical argument for investment diversification

The mathematical argument for investment diversification

You may hear financial advisers say that you should have a diversified investment portfolio, but why? Just to spread the risk and not to “have all your eggs in one basket”? Does this not just lead to average investment performance if we are just spreading risk for the sake of it? These are common misconceptions and this article will use mathematical arguments to explain why diversification has been described as “the only free lunch” by finance and economics researchers.

A simple example of investment diversification: a one asset vs a two asset investment portfolio

If we take two shares, Company A and Company B and let’s say that analysts for both shares expect a total investment return (share price growth + dividends) of 5% for 2024. Let’s also say that you have 100,000 euros to invest. If you put all of your 100,000 euros into just one of these stocks, then your expected return is €5,000 as the expected return is simply the sum of the weighted expected returns of the portfolio. However, if you invest 50,000 into Company A and 50,000 into Company B, your expected return is still €5,000 but you are now less exposed to the non-market or industry-wide risks of one of these companies, such as the board of directors dying in an accident. This kind of company specific risk is called unsystematic risk, diversifiable risk or specific risk.

Can we quantify the risks and the effects of investment diversification on risk?

Yes, although we cannot predict the future, we can measure the past volatility of a stock by calculating something called the standard deviation. The standard deviation is based upon the daily returns of a stock and the difference between these daily returns and the average return of that stock, or the deviation from the average.

Standard deviation:

σ = the standard deviation
μ = the mean of all the values
xᵢ = the individual x values
N = the number of data points

Modern Portfolio Theory

This part of the explanation is where we should talk about Harry Markowitz’s Nobel Prize winning research on investment portfolio selection, published in the Journal of Finance in 1952, which is known as Modern Portfolio Theory.

This theory assumes that investors are rational and that they want the greatest return for any given level of risk. So if we take our two asset portfolio, let’s say that the annual volatility of Company A is 10% and for Company B it is 9%, then shouldn’t we just put all of our €100,000 investment into Company B, considering that they have the same expected return? The mathematical answer is probably not, because we haven’t considered the covariance and the correlation of these two stocks, in other words: these two stocks do not always move in exactly the same direction on the same days, weeks, months or years and by the same amounts. The correlation of this stock pair is part of the formula for calculating the standard deviation of the portfolio:

Formula for the standard deviation of a two asset portfolio:

Formula for the correlation coefficient (replacing 1,2 with x and y):

\rho _{X,Y}={\frac {\operatorname {cov} (X,Y)}{\sigma _{X}\sigma _{Y}}}

where

$\operatorname {cov}$ is the covariance
$\sigma _{X}$ is the standard deviation of $X$
$\sigma _{Y}$ is the standard deviation of $Y$

If the correlation between these two stocks is 0.5 then the standard deviation of a portfolio invested 50% into each stock is 8.23%, which mathematically shows that diversifying can allow us to reduce the risk of an investment portfolio to sometimes even below that of the least riskiest individual asset. A diversified portfolio will be less risky than the sum of its individual parts as long as the assets are not perfectly positively correlated with each other. This is something that many people fail to consider when they criticise diversification and just invest into a handful of different companies. In this example, diversification has allowed us to reduce the volatility of the investment with no reduction in expected return.

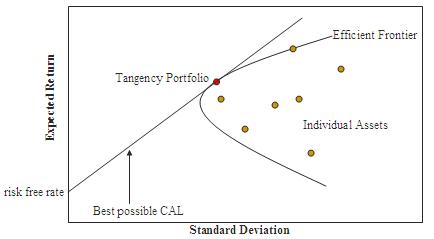
Also, just because we can lower the volatility of my example portfolio by investing 50% into each stock, this does not mean that 50% into each stock is what you should invest, why not 60% in one and 40% in the other? To which one should we give the larger weighting? The answer to this question is beyond the scope of this blog post, but to simplify, we need to analyse the expected returns and risks of many different portfolio combinations and then choose a portfolio which is on the “efficient frontier” which represents the portfolios with the highest possible expected return for each given level of risk, in this case measured by standard deviation.

Investment volatility cannot be accurately predicted by analysing past volatility, but Modern Portfolio Theory and academic research shows that there is a mathematical argument for investment diversification and it should not be avoided for fear of having “average” returns.

How Aisa International can help you with investment diversification?

We only offer diversified investment portfolios, of different levels of risk, with no hidden charges. Feel free to contact us at support@aisainternational.fr for an investment and financial review.

Useful links:

The views expressed in this article are not to be construed as personal advice. Therefore, you should contact a qualified, and ideally, regulated adviser in order to obtain up-to-date personal advice with regard to your own personal circumstances. Consequently, if you do not, then you are acting under your own authority and deemed “execution only”. Additionally, the author does not accept any liability for people acting without personalised advice, who base a decision on views expressed in this generic article. Importantly, this article is dated and is based on legislation as of the date. It should be noted that legislation changes, but articles are rarely updated. Sometimes a new article is written; so, please check for later articles. Additionally, check for changes in legislation on official government websites. Finally, this article should not be relied on in isolation.

Contact Us